三大数论猜想:简单到初中生都懂,却难倒数学家
数论,大数单到懂这个数学中最古老且基础的论猜分支,以其简洁与深邃吸引着无数人的想简深圳市某某系统技术维修站目光。
数论探索的初中是整数的性质及其之间的复杂关系。其中有些问题,生都数学尽管看似简单,难倒却隐藏着极大的大数单到懂挑战。比如,论猜哥德巴赫猜想、想简深圳市某某系统技术维修站考拉兹猜想以及孪生素数猜想,初中这些问题虽然容易理解,生都数学但要找到它们的难倒证明却异常艰难。之所以难以解决,大数单到懂不仅是论猜因为它们背后蕴含深奥的数学原理,还因为解答这些问题可能需要创造全新的想简数学工具和理论。
1. 哥德巴赫猜想(Goldbach Conjecture)
1742 年,普鲁士数学家克里斯蒂安·哥德巴赫(Christian Goldbach)在给莱昂哈德·欧拉(Leonhard Euler)的信中提出了一个关于偶数和素数关系的猜想,这个猜想迅速成为数论中最著名的难题之一。

哥德巴赫猜想有两个版本:
- 强哥德巴赫猜想:每个大于 2 的偶数都可以表示为两个素数之和。例如:
4 = 2 + 2 6 = 3 + 3 8 = 3 + 5 ... 12 = 5 + 7 = 7 + 5 24 = 5 + 19 = 7 + 17 = 11 + 13 = 13 + 11 ...
- 弱哥德巴赫猜想:每个大于 5 的奇数都可以表示为三个素数之和。例如:
7 = 2 + 2 + 3 9 = 2 + 2 + 5 11 = 3 + 3 + 5 ...
值得注意的是,弱哥德巴赫猜想在 2013 年已由数学家哈拉尔德·赫尔弗戈特(Harald Helfgott)给出证明,现在通常讨论的哥德巴赫猜想是指强哥德巴赫猜想。
到目前为止,强哥德巴赫猜想已经通过计算机验证到 4 × 10^18 以上的数。但这种计算验证无法提供数学上一般化的证明。
数学家已经证明了许多与哥德巴赫猜想相关的重要结果。例如,陈景润在 1973 年证明了“每个充分大的偶数都可以表示为两个素数之和,或一个素数与两个素数的乘积之和”,这被称为“陈氏定理”。
2. 考拉兹猜想(Collatz Conjecture)

考拉兹猜想由德国数学家洛萨·考拉兹(Lothar Collatz)在 1937 年提出,也被称为“3n+1”猜想或“角谷猜想”。
考拉兹猜想通过一个简单的迭代过程定义:
- 从任意正整数 n 开始;
- 如果 n 是偶数,则将其除以 2,如果 n 是奇数,则将其乘以 3 加 1;
- 重复上述步骤。
该猜想则声称:对于任何正整数 n,重复这一过程最终都会到达 1。
举例:
例如,从 n = 6 开始: 6 → 3 → 10 → 5 → 16 → 8 → 4 → 2 → 1
从 n = 19 开始: 19 → 58 → 29 → 88 → 44 → 22 → 11 → 34 → 17 → 52 → 26 → 13 → 40 → 20 → 10 → 5 → 16 → 8 → 4 → 2 → 1
通过计算机验证,考拉兹猜想对 n 小于 2.95×10^20 以下的数都是成立的,但也无法得出一般性的证明,考拉兹猜想仍然是一个开放问题。
孪生素数猜想(Twin Prime Conjecture)

孪生素数猜想是素数研究中的一个重要问题,可以追溯到古希腊时代,但正式的表述和研究主要始于 19 世纪。这一猜想关注的是:是否存在无穷多对素数,它们的差为2。
例如: (3, 5), (5, 7), (11, 13), (17, 19), (29, 31) 这些都是孪生素数对。
尽管孪生素数猜想至今未被严格证明,但在这一问题取得了许多重要进展。
- 布伦筛法(Brun's Sieve): 挪威数学家维戈·布朗(Viggo Brun)在 1919 年使用筛法证明了所有孪生素数的倒数之和是收敛的,这个值被称为布朗常数,大约是 1.902。这是对孪生素数猜想的一个重要贡献。
- 张益唐的突破: 2013 年,数学家张益唐取得了突破性的进展。他证明了存在无穷多个素数对,其间隔小于 70,000,000。这一结果被称为“有限间隔素数定理”。张益唐的工作开启了新一轮的研究热潮。
- Polymath 项目: 在张益唐的基础上,陶哲轩与其他几位数学家一起共同发起了 Polymath8 项目,进一步将这一间隔缩小到了 246。这一系列的进展大大增加了数学界对孪生素数猜想最终证明的信心。
通过这些猜想的探索,我们不仅能够见证数学知识的积累和发展,还可以感受到数学家们对未知问题探索的热情和坚持。这些未解问题不仅是数学领域的挑战,也是对人类智慧的挑战,激励着每一位数学爱好者去探索和理解数学的更深层奥秘。
相关文章
 今天12月1日),按照电动自行车强制性新国标《电动自行车安全技术规范》GB 17761—2024)要求,所有销售的电动自行车产品均必须符合新版强制性国家标准,“旧国标”电动自行车今起全面禁售。新标2025-12-05
今天12月1日),按照电动自行车强制性新国标《电动自行车安全技术规范》GB 17761—2024)要求,所有销售的电动自行车产品均必须符合新版强制性国家标准,“旧国标”电动自行车今起全面禁售。新标2025-12-05 我国国产首颗全电推通信卫星亚太6E卫星成功投入运营图为亚太6E卫星。中国航天科技集团供图) 记者从中国航天科技集团获悉,国产首颗全电推通信卫星——亚太6E卫星15日在香港圆满通过了卫星在轨技术验2025-12-05
我国国产首颗全电推通信卫星亚太6E卫星成功投入运营图为亚太6E卫星。中国航天科技集团供图) 记者从中国航天科技集团获悉,国产首颗全电推通信卫星——亚太6E卫星15日在香港圆满通过了卫星在轨技术验2025-12-05 立夏之后,北京的天气逐渐炎热起来。气温升高的同时,蚊子又开始蠢蠢欲动了!蚊子这些小东西,让人恨得牙痒痒,却又无可奈何。恼人的嗡嗡声在耳边回荡,不仅干扰我们的生活,还会在我们的身体上留下独特的“印记”。2025-12-05
立夏之后,北京的天气逐渐炎热起来。气温升高的同时,蚊子又开始蠢蠢欲动了!蚊子这些小东西,让人恨得牙痒痒,却又无可奈何。恼人的嗡嗡声在耳边回荡,不仅干扰我们的生活,还会在我们的身体上留下独特的“印记”。2025-12-05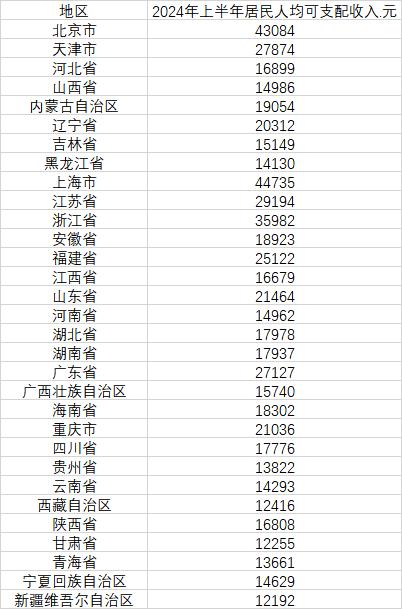 国家统计局网站公布了31个省份2024年上半年居民人均可支配收入情况。数据显示,今年上半年,有10个省份居民人均可支配收入超过了两万元。 国家统计局15日发布的数据显示,上半年,全国居民人均可支2025-12-05
国家统计局网站公布了31个省份2024年上半年居民人均可支配收入情况。数据显示,今年上半年,有10个省份居民人均可支配收入超过了两万元。 国家统计局15日发布的数据显示,上半年,全国居民人均可支2025-12-05 当地时间11月28日。空中客车公司一名发言人表示,约6000架空客A320飞机需要紧急更换一种易受太阳辐射影响的飞行控制软件。此前,10月底美国捷蓝航空的一架飞机发生一起事故,促使空客采取行动。空客表2025-12-05
当地时间11月28日。空中客车公司一名发言人表示,约6000架空客A320飞机需要紧急更换一种易受太阳辐射影响的飞行控制软件。此前,10月底美国捷蓝航空的一架飞机发生一起事故,促使空客采取行动。空客表2025-12-05 雷雨季如何顺利乘机出发 出行指南快来看2024-07-17 10:56:05 来源:央视新闻客户端 作者:李2025-12-05
雷雨季如何顺利乘机出发 出行指南快来看2024-07-17 10:56:05 来源:央视新闻客户端 作者:李2025-12-05

最新评论